10月7日，瑞典皇家科学院公布了2025年诺贝尔物理学奖获得者。三位量子物理领域的科学家：加州大学伯克利分校教授约翰·克拉克（John Clarke）、耶鲁大学教授米歇尔·德沃雷（Michel H. Devoret）以及加州大学圣巴巴拉分校教授约翰·马蒂尼斯（John M. Martinis），由于“发现电路中的宏观量子力学隧穿效应和能量量子化（for the discovery of macroscopic quantum mechanical tunnelling and energy quantisation in an electric circuit）”的成就而获奖。

Ill. Niklas Elmehed © Nobel Prize Outreach

三位科学家于1984年至1985年间，首次在宏观电路中观测到量子隧穿与能量量子化，为量子力学从“微观理论”走向“宏观技术”打开了大门，并开辟了超导量子电路和超导量子比特这一技术路线，奠定了超导量子计算的科学原理基础；而后续超导量子计算的蓬勃发展，又回过头来促使这项40年前的基础科学发现最终得到了诺贝尔物理学奖的青睐。

一、首次证实宏观量子隧穿效应

量子隧穿效应是量子力学预言的微观粒子与宏观世界最显著的区别之一。当一个粒子的动能小于势垒时，经典物理学认为这个粒子将不能穿过势垒（类似于物体不能穿过墙壁），而量子力学则允许粒子以一定的概率穿透势垒。然而，一旦涉及大量粒子，量子力学效应就变得非常微弱，因此通常认为在宏观世界无法观测到量子隧穿效应。

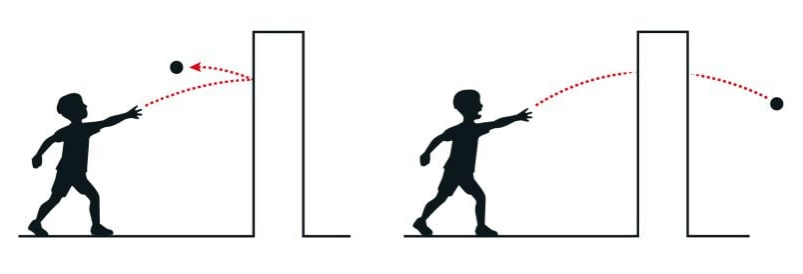
量子隧穿的形象描述（图右）

© Johan Jarnestad/瑞典皇家科学院

20世纪80年代初，安东尼·莱格特（Anthony Leggett，2003年诺贝尔物理学奖获得者）预言：在约瑟夫森结超导电路中可能展现宏观尺度的量子隧穿^[1]。1984 至 1985 年间，三位获奖者进行了一系列开创性实验。他们通过电流偏置的约瑟夫森结成功观测到了大量电子的集体量子行为，首次定量证实了宏观量子隧穿的存在^[2]。后续他们还通过微波谱学技术观测到了约瑟夫森结中宏观量子系统的能级量子化，进一步证明了整个电路的宏观行为就如同单一粒子一样呈现出显著的量子效应^[3]。

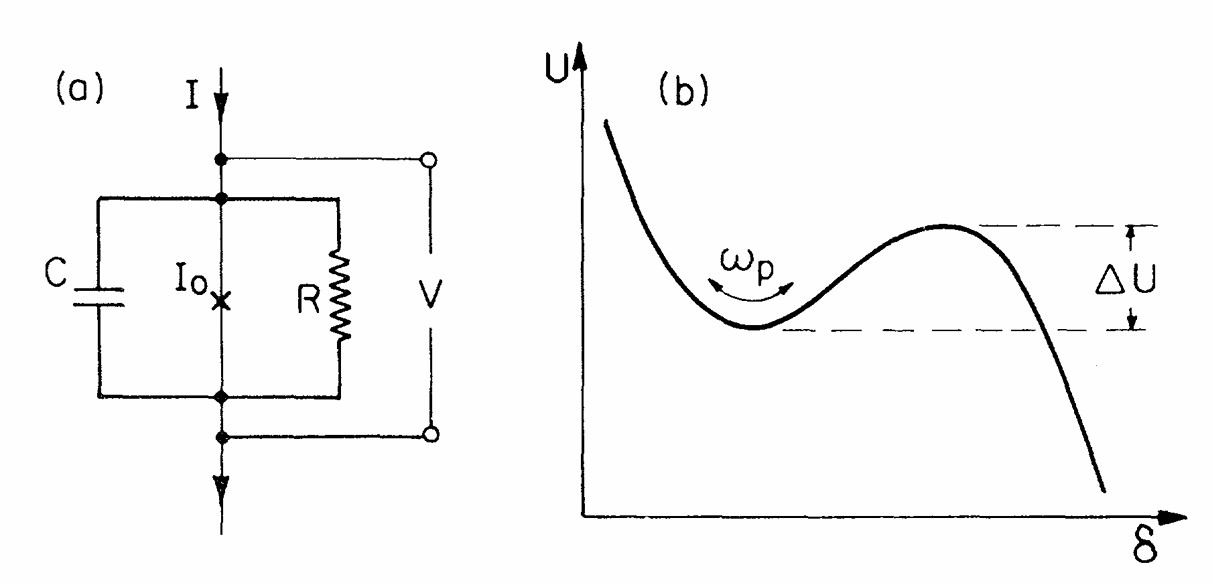
首次观测到宏观量子隧穿效应的约瑟夫森结示意图

© Physical Review Letter 53, 1260 (1984)

这一发现突破了“量子力学仅适用于微观世界”的直观感受，表明由大量粒子组成的宏观系统仍可保持量子相干性，并表现出可观测的量子行为。

二、超导量子比特与量子计算的发展

约瑟夫森结宏观量子隧穿的证实，表明超导电路系统可以被视为一种“大型人工原子”，具备明确的量子态、能级结构和可控的量子跃迁，可连接外部电路作为可控的量子单元用于更复杂的实验系统，为后续超导量子比特的发展奠定了科学基础。包括三位获奖者在内的多位科学家开展了系列工作，使得40年前的基础科学发现演变成强大的计算能力。

1. 初步构建超导量子比特。1997年到1998年间，德沃雷团队研制出一种被称为“库珀对盒（Cooper pair box）”的微型电路^[4]，并证明其基态是电荷量子态的叠加（该器件后来被称为电荷量子比特），初步构建了超导量子比特^[5]。于此同时，日本电气株式会社（NEC）的中村泰信（Yasunobu Nakamura）、陈启东（Chii-Dong Chen）和蔡兆申（Jaw Shen Tsai）在微波光谱中观察到超导单电子晶体管的能级反交叉现象，作为电荷态叠加的证据^[6]。

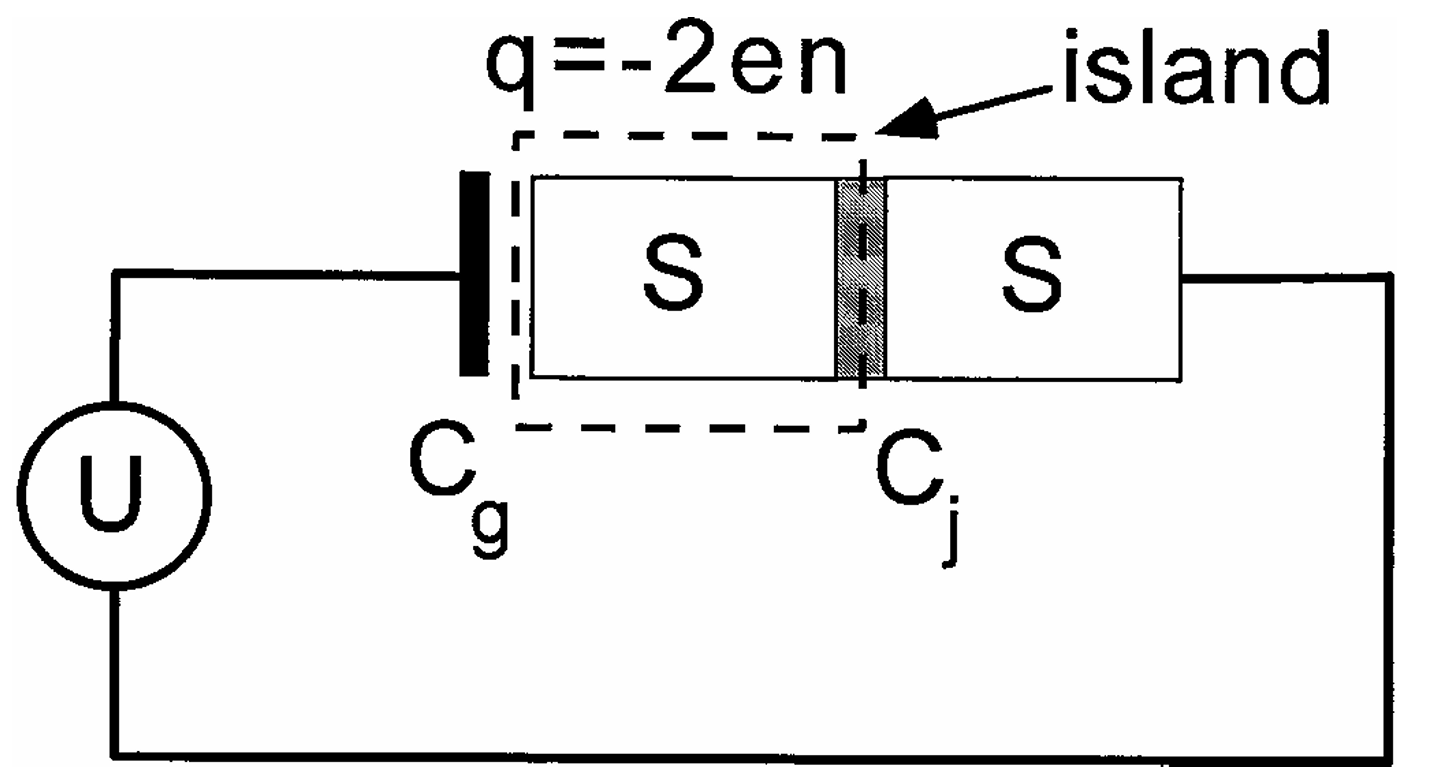
库珀对盒微型电路示意图

© Physica Scripta, T16, 165 (1998)

2. 实现超导量子比特的相干操控。1999年，中村泰信、Yuri Pashkin和蔡兆申在库珀对盒子中演示了基态“0”与激发态“1”之间的拉比振荡^[7]。这一实验使得凝聚态物理界认识到可控超导量子比特可能性。

3. 实现超导量子比特的完整操控。2002年，德沃雷团队对电荷量子比特进行改进研制出quantronium量子比特，将相干时间提升了两个数量级，不仅实现了拉比振荡（幅度振荡），还演示了Ramsey振荡（相位振荡）^[8]。用量子信息的语言表述，这一成果标志着具备了完整精确的单超导量子比特操控能力。

4. 实现高保真、长相干的量子操控。此后，超导量子比特家族不断扩展，除了前述的电荷量子比特和quantronium量子比特外，还包括：Hans Mooij和中村泰信等发展的磁通量子比特（flux qubit）^[9]，马蒂尼斯发展的相位量子比特（phase qubit）^[10]，德沃雷、Robert Schoelkopf和Steven Girvin等发展的transmon量子比特^[11]以及德沃雷等发展的fluxonium量子比特^[12]等。经过25年的发展，超导量子比特的相干时间提高了六个数量级，成为实现量子计算的有力候选者。当前最常用的超导器件设计基于transmon量子比特与电路量子电动力学（circuit QED）架构^[13-15]，通过将超导量子比特与微波谐振腔耦合实现高保真、长相干的量子操控。

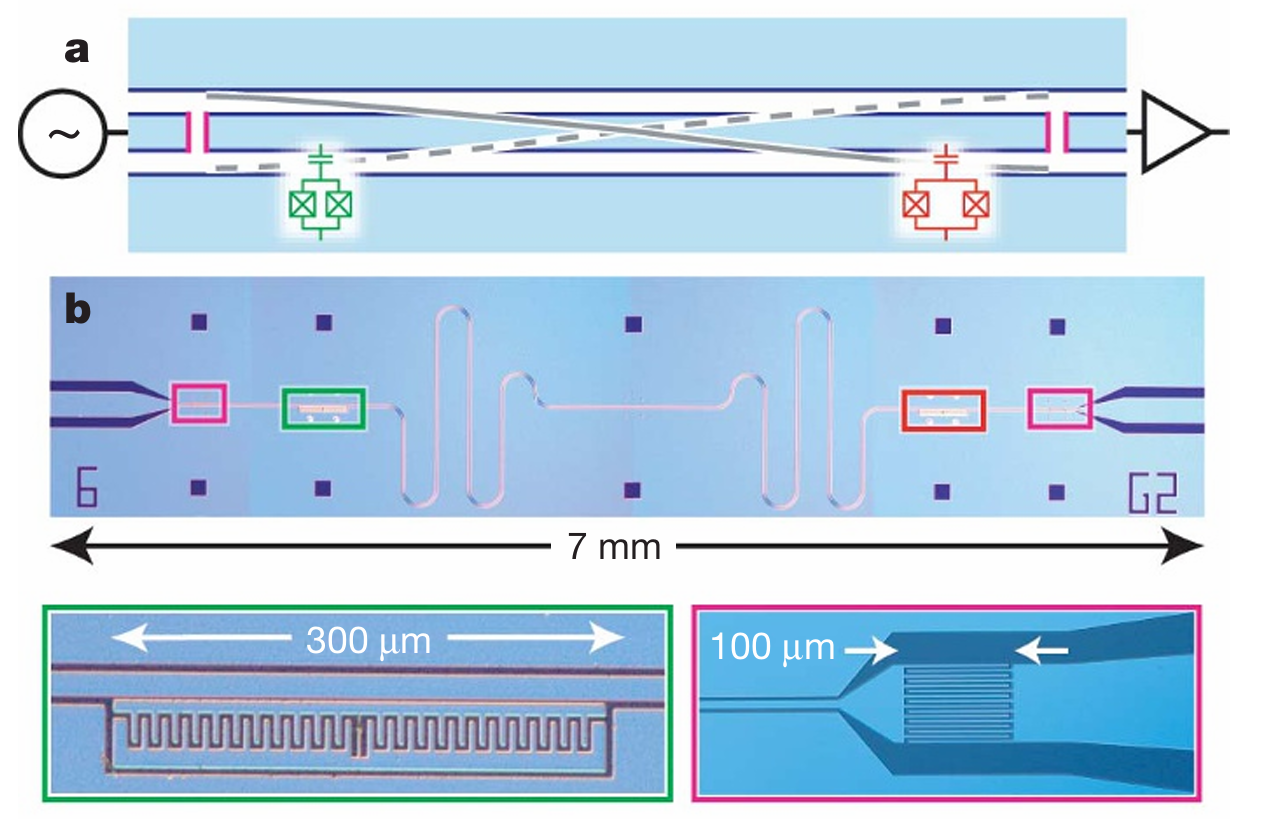
微波谐振腔耦合的两个超导量子比特

© Nature 449, 443 (2007)

三、量子计算优越性的实现与竞争

在超导量子比特方面的技术突破推动了超导量子计算成为现实。在量子计算的发展过程中，“量子计算优越性”是第一个里程碑。“量子计算优越性”验证了量子计算系统能够超越传统超级计算机的可行性，是量子计算具备应用价值的前提条件，也是当前一个国家量子计算研究实力的直接体现。

2014年至2020年期间，马蒂尼斯加入谷歌量子人工智能实验室，负责超导量子计算研发。2019年，谷歌率先宣称实现“量子计算优越性”：其53比特“悬铃木（Sycamore）”处理器在200秒内完成的随机线路采样任务，用当时最快的超级计算机进行模拟需要约一万年^[16]。量子计算优越性的首次展示推动了国际上对量子计算研究的空前重视，主要国家的政府和多家科技巨头企业都加强了对超导量子计算的部署和投入。

谷歌53比特“悬铃木”超导量子处理器

© Google

不过，大规模超导量子比特的集成和操纵是高度复杂的系统工程，到目前全球只有谷歌和合肥国家实验室实现了超导体系的量子计算优越性。

尽管谷歌在2019年率先宣称了量子计算优越性，但合肥国家实验室后续演示了更先进的经典算法，用1400余块A100 GPU仅需约14秒即可完成2019年“悬铃木”同样的任务，因此谷歌当时的宣称已被合肥国家实验室推翻^[17]。而以最优的经典算法为比较标准，超导体系首个被严格证明并保持至今的量子计算优越性由合肥国家实验室于2021年在66比特的“祖冲之二号”处理器上实现^[18]。

合肥国家实验室66比特“祖冲之二号”超导量子处理器

2024年，谷歌实现了72比特的升级版“悬铃木”，求解随机线路采样任务的速度比最快的超级计算机快10⁹倍（即优势比为10⁹）^[19]。2025年，合肥国家实验室 105比特“祖冲之三号”的优势比达到了10¹⁵，超过升级版“悬铃木”6个数量级，为目前超导体系公开发表的最强量子计算优越性^[20]。

合肥国家实验室105比特“祖冲之三号”超导量子处理器

四、小结

目前，超导量子体系已成为最有希望实现规模化量子计算的物理体系之一，国际学术界和产业界普遍预期到2035年前后有望达到100万个超导量子比特的相干操纵，进而构建容错通用量子计算机。

迄今，超导量子计算的发展可分为三个阶段：

1. 基础原理的建立。克拉克、德沃雷以及马蒂尼斯首次在宏观电路中观测到量子隧穿与能量量子化，奠定了超导量子比特和超导量子计算的科学基础。

2. 超导量子比特的实现。德沃雷以及中村泰信等开创了超导量子电路和量子比特一系列早期关键技术，使得超导量子计算成为现实。

3. 量子计算优越性的实现。随着超导量子比特技术的成熟，马蒂尼斯带领的谷歌团队率先在超导量子计算的规模化工程现实方面取得突破，首次达到了量子计算优越性里程碑。随后，合肥国家实验室和谷歌呈现交替领先的态势。

值得一提的是，此前克拉克、德沃雷以及中村泰信由于“开创了超导量子电路和量子比特一系列早期关键技术”而获得了2021年度“墨子量子奖”。“墨子量子奖”由安徽墨子量子科技基金会于2018年设立，由国内民间企业家捐资支持，旨在表彰国际上在量子通信、量子计算与模拟和量子精密测量等领域做出杰出贡献的科学家。着眼于量子信息科技，“墨子量子奖”评审委员会综合考虑了超导量子计算的发展阶段，对前期从基础科学发现到关键技术突破过程中这三位有代表性的学者进行了表彰。

2021年度“墨子量子奖”获奖者

除克拉克与德沃雷外，多位墨子量子奖获得者在后续获得了重要的国际学术大奖，包括：2018年度获奖者戴维·多伊奇（David Deutsch）和彼得·绍尔（Peter Shor）、2019年度获奖者查理斯·本内特（Charles Bennett）和吉勒斯·巴萨德（Gilles Brassard）获2023年度科学突破奖（Breakthrough Prize）；2019年度奖获奖者安东·蔡林格（Anton Zeilinger）获得2022年诺贝尔物理学奖；2020年度获奖者香取秀俊和叶军获2022年度科学突破奖。“墨子量子奖”的预见性体现了该奖已经成为量子信息与量子技术领域最具国际影响力的学术奖项。

参考文献：

[1] A. Leggett, “Macroscopic Quantum Systems and the Quantum Theory of Measurement”, Progress of Theoretical Physics Supplement, 69, 80 (1980); A. O. Caldeira and A. J. Leggett, “Influence of Dissipation on Quantum Tunneling in Macroscopic Systems”, Phys. Rev. Lett. 46, 211 (1981).

[2] M. H. Devoret, J. M. Martinis, D. Esteve and J. Clarke, “Resonant Activation from the Zero-Voltage State of a Current-Biased Josephson Junction”, Phys. Rev. Lett. 53, 1260 (1984).

[3] J. M. Martinis, M. H. Devoret and J. Clarke, “Energy-Level Quantization in the Zero-Voltage State of a Current-Biased Josephson Junction”, Phys. Rev. Lett. 55, 1543 (1985).

[4] V. Bouchiat, PhD thesis 1997 (Paris 6 University).

[5] V. Bouchiat et al., Quantum Coherence with a single Cooper Pair, Physica Scripta, T16, 165 (1998).

[6] Nakamura, Chen, and Tsai, “Spectroscopy of Energy-Level Splitting between Two Macroscopic Quantum States of Charge Coherently Superposed by Josephson Coupling”, Phys. Rev. Lett. 79, 2328 (1997).

[7] Y. Nakamura, Y. Pashkin and J. S. Tsai, “Coherent control of macroscopic quantum states in a single-Cooper-pair box”, Nature 398, 786, (1999).

[8] D. Vion et al., “Manipulating the Quantum State of an Electrical Circuit”, Science, 296, 886 (2002).

[9] I. Chiorescu et al., “Coherent quantum dynamics of a superconducting flux qubit”, Science 299, 1869 (2003).

[10] J. Martinis, “Superconducting phase qubits”, Quantum Inf. Process. 8, 81 (2009).

[11] J. Koch et al., “Charge-insensitive qubit design derived from the Cooper pair box”, Phys. Rev. A 76, 042319 (2007).

[12] V. Manucharyan et al., “Fluxonium: Single Cooper-Pair Circuit Free of Charge Offsets”, Science 326, 113 (2009).

[13] A. Blais et al., “Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation”, Phys. Rev. A 69, 062320 (2004).

[14] Wallraff et al., “Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics”, Nature 431, 162 (2004).

[15] J. Majer et al., “Coupling superconducting qubits via a cavity bus”, Nature 449, 443 (2007).

[16] F. Arute et al., “Quantum supremacy using a programmable superconducting processor”, Nature 574, 505 (2019).

[17] X. -H. Zhao et al., “Leapfrogging Sycamore: harnessing 1432 GPUs for 7×faster quantum random circuit sampling”, National Science Review, nwae317 (2024).

[18] Y. Wu et al., "Strong quantum computational advantage using a superconducting quantum processor", Phys. Rev. lett. 127, 180501 (2021).

[19] A. Morvan et al., “Phase transitions in random circuit sampling”, Nature 634, 328 (2024).

[20] D. Gao, et al., “Establishing a new benchmark in quantum computational advantage with 105-qubit zuchongzhi 3.0 processor”, Phys. Rev. lett. 134, 090601 (2025).

信息来源：“量子科话”微信公众号