当你在区块链网络发起一笔比特币交易时，一串看不见的密码学协议正在默默守护资产安全。这道安全屏障的核心，是椭圆曲线密码学（ECC），一种基于“椭圆曲线离散对数问题”的经典加密方案。然而，量子计算的崛起正悄然改写游戏规则：Shor算法的出现，让原本经典计算机无法破解的数学难题，在足够强大的量子计算机面前变得可行。

2025年10月27日，清华大学马雄峰团队在预印平台arxiv上发表题为”Resource analysis of Shor's elliptic curve algorithm with an improved quantum adder on a two-dimensional lattice”（在二维晶格上对Shor椭圆曲线算法的资源分析，采用改进的量子加法器）的研究论文，顾全、叶涵、陈俊杰为论文共同第一作者，马雄峰为论文通讯作者。

该研究首次针对二维晶格架构的量子计算机，完成了Shor椭圆曲线算法的全面资源分析，为量子攻击密码系统提供了最接近现实的技术基准，也让“量子计算机何时能破解比特币”这个问题有了更明确的答案。

01 背景

在数字时代，密码学是守护隐私与资产的核心防线。我们日常使用的网络支付、数字签名，以及比特币等加密货币，都依赖公钥密码体系。其中，椭圆曲线密码（ECC）凭借高效性成为主流选择，比特币采用的secp256k1曲线、NIST推荐的P-256/P-384/P-521曲线，均是全球数十亿设备的安全基石。这些系统的安全性，建立在一个关键假设之上：经典计算机无法在合理时间内解决“椭圆曲线离散对数问题”，简单来说，就是无法从公开的公钥反推出核心的私钥。

1994年，Shor算法的诞生打破了这一平衡。作为量子计算领域的里程碑成果，它能在多项式时间内求解离散对数问题，相比经典算法实现指数级加速。这意味着，一旦量子计算机达到足够规模，当前绝大多数公钥密码体系都将被破解。更严峻的是，比特币等加密货币面临双重威胁：一方面，历史上已公开公钥的钱包（据估计包含超620万枚比特币），一旦私钥被量子计算机反推，资产将被直接窃取；另一方面，新交易广播时暴露的公钥，可能被攻击者利用量子计算机抢先伪造交易，截获转账资金。

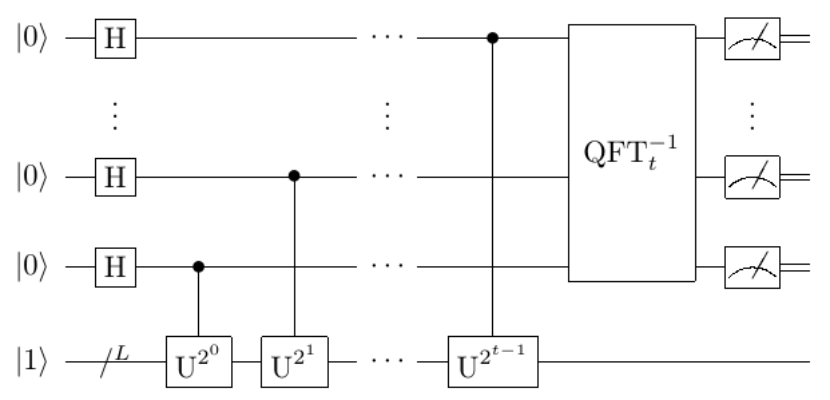
尽管威胁真实存在，但长期以来，关于Shor椭圆曲线算法的实用化研究仍存在明显缺口。现有研究要么聚焦于整数分解问题，要么忽略量子硬件的实际约束。当前主流量子平台（如超导量子比特、拓扑量子比特）均采用二维nearest-neighbor（最近邻）布局，无法实现任意两个量子比特的直接连接，这会大幅增加长距离门的路由开销。此外，量子加法器作为Shor算法的核心组件，长期存在“深度-空间”权衡难题：传统进位前瞻加法器要么需要O(nlog n)个辅助量子比特（空间开销过大），要么Toffoli深度高达4log n（时间开销过高），难以适配NISQ（噪声中等规模量子）时代的硬件限制。

清华大学团队的研究正是瞄准这些痛点，在二维晶格架构下优化Shor椭圆曲线算法，给出了破解主流椭圆曲线密码的具体资源需求，为量子计算的实际应用与密码学防御提供了关键参考。

02 理论方法：三大核心创新突破技术瓶颈

要让Shor椭圆曲线算法在现实量子硬件上实现，必须解决三个核心问题：适配二维晶格的算术组件设计、长距离门的高效实现、以及全流程的资源优化。团队通过三大技术创新，构建了一套兼顾效率与可行性的解决方案。

（一）改进型量子加法器：兼顾深度与空间效率

量子加法器是Shor算法中最基础也最关键的组件。椭圆曲线运算的核心是模块化算术，而加法器的性能直接决定了整个算法的资源开销。此前，行业内存在两种主流加法器：一种是Brent-Kung树加法器，虽仅需O(n)个辅助量子比特，但Toffoli深度高达4log n；另一种是Sklansky树加法器，能将深度降至2log n，却需要O(nlog n) 个辅助量子比特，这对于量子比特稀缺的硬件来说难以承受。

团队提出的新型进位前瞻量子加法器，巧妙结合了两种方案的优势：通过分块计算进位（块内用Brent-Kung树，块间用Sklansky树），在仅使用O(n)个辅助量子比特的前提下，将Toffoli深度优化至log n+log log n+O (1)。更重要的是，该设计天然适配二维最近邻架构，仅引入常数级的额外开销。具体来说，对于n位输入的加法运算，新型加法器仅需6n个量子比特，Toffoli数量约14n，相比传统方案，在空间开销不变的情况下，深度几乎减半，为后续算法的高效实现奠定了基础。

（二）动态电路技术：突破二维晶格的连接限制

二维晶格架构的核心约束是“最近邻”，量子比特只能与相邻的量子比特进行交互，长距离门需要通过交换量子比特（SWAP门）实现，这会带来巨大的深度开销。为解决这一问题，团队引入了动态电路技术，通过“中间测量+经典控制+前馈操作”的组合，在常数开销下实现长距离门。

动态电路的核心思想是“用时间换空间”：在电路运行过程中，对辅助量子比特进行中间测量，将测量结果用于控制后续量子门的操作。这种方式无需额外增加量子比特，就能实现长距离CNOT门、长距离Toffoli门等关键组件。例如，要实现两个远距离量子比特的Toffoli门，传统方案需要多次SWAP门，深度随距离线性增加；而动态电路通过相邻辅助量子比特的链式测量与控制，仅需常数深度就能完成。此外，团队还利用动态电路实现了无界GHZ态生成，让多个受控门可以并行执行，进一步降低了电路深度。

（三）算法级优化：整合窗口法与蒙哥马利表示

除了硬件适配，算法层面的优化同样关键。团队将窗口法、蒙哥马利表示和量子查表等技术整合进Shor算法，大幅降低了整体资源开销。窗口法的核心是“批量处理比特”，传统方案需要2n次受控点加法，而窗口法将l个比特分为一组，每次处理一组，可减少(l-1)次点加法，仅需额外维护一个量子查表；蒙哥马利表示则简化了模块化乘法的计算流程，避免了复杂的除法操作；量子查表则通过预存储计算结果，快速调用所需的中间值，减少重复运算。

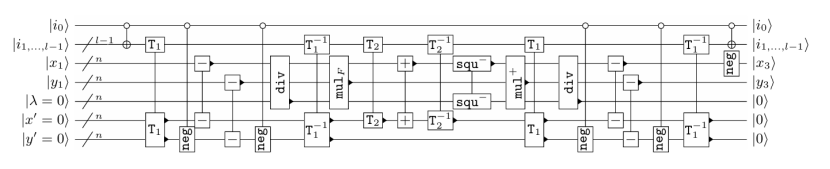
这些技术的整合，让Shor椭圆曲线算法在二维晶格架构下的开销大幅降低。例如，窗口大小选择log n时，点加法的数量可减少一个数量级，而量子查表的额外开销仅为常数级，最终实现了“时间-空间”的最优平衡。

（四）二维晶格布局：适配现实量子硬件

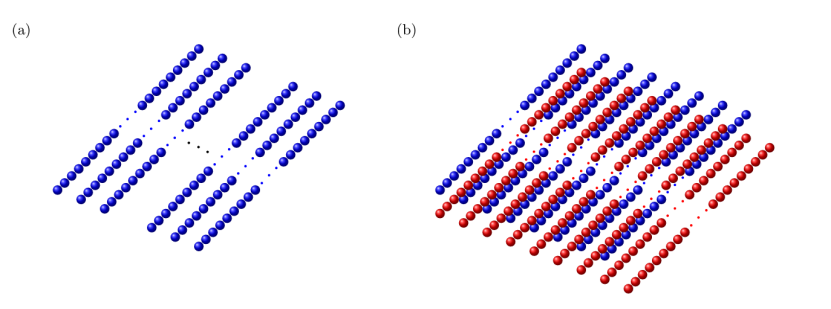
为了让方案具备可实现性，团队设计了两种二维晶格布局：单层n×17晶格和双层n×9×2晶格。两种布局均包含17n个量子比特，其中2n个用于存储点加法结果，13n个用于中间计算，2n个作为辅助量子比特。双层布局通过上下层的交叉连接，能更高效地实现最近邻门；单层布局则更适配现有量子硬件，仅需少量SWAP门即可补偿连接限制，两种布局的门交互距离均控制在常数范围内，避免了额外的深度开销。

03 实验结果：破解P-256曲线需4300个逻辑量子比特

基于上述技术方案，团队对Shor椭圆曲线算法进行了全面的资源分析，涵盖了从25位到521位的多种输入规模（对应不同安全级别的椭圆曲线），给出了量子比特数量、CNOT门深度与数量、Toffoli门深度与数量等关键指标的精确估计。

对于密码学领域最受关注的NIST P-256曲线（比特币secp256k1曲线的安全级别与之相当），破解它需要约4300个逻辑量子比特，Toffoli门的保真度需达到10^-9级别。具体来说，对应的CNOT门深度约1.89×10⁷，CNOT门数量约2.89×10⁹，Toffoli门深度约1.09×10⁷，Toffoli门数量约1.33×10⁹。

为了让读者更直观地理解资源需求，我们可以对比不同输入规模的核心指标：破解25位椭圆曲线仅需425个逻辑量子比特，32位曲线需544个，而破解更高级别的P-384曲线则需要7528个逻辑量子比特，P-521曲线需要8857个逻辑量子比特。从趋势上看，量子比特数量与输入规模呈线性关系（约17n），而门数量则呈多项式增长，这符合Shor算法的理论特性。 

值得注意的是，团队的资源估计考虑了现实硬件的所有约束：包括二维晶格的最近邻限制、动态电路的中间测量开销、以及模块化算术的全流程优化。这些结果并非纯理论推导，而是基于实际电路设计的精确计算，为后续量子硬件的研发和密码学防御策略的制定提供了可落地的参考基准。

04 研究成果：重新定义量子密码攻击的技术边界

这项研究的价值不仅在于给出了一组精确的资源数据，更在于为量子计算与密码学的交叉领域提供了三大关键突破，重新定义了量子密码攻击的技术边界。

（一）建立了二维晶格下的Shor算法资源基准

此前的Shor算法资源分析多基于“全连接”假设，即量子比特可以任意连接，这与现实量子硬件的二维晶格架构存在巨大差距。团队首次在真实硬件约束下完成了全流程资源分析，证明了Shor椭圆曲线算法在二维晶格上实现的可行性，给出的量子比特数量、门深度等指标，成为行业内首个贴近现实的技术基准。这意味着，未来量子硬件研发可以以此为目标，明确“破解密码所需的最小量子计算机规模”。

（二）新型加法器具备广泛的普适性

团队提出的改进型量子加法器，不仅适用于Shor椭圆曲线算法，还可应用于所有需要模块化算术的量子算法。包括整数分解、晶格问题、量子模拟等。由于其兼顾深度与空间效率，且适配二维架构，有望成为量子算术的“标准组件”，推动各类量子算法的实用化进程。

（三）揭示了椭圆曲线与RSA的量子攻击差异

经典密码学中，256位椭圆曲线的安全级别与3072位RSA相当，但量子攻击的难度却大不相同。团队的分析显示，破解256位椭圆曲线需要约4300个逻辑量子比特，而破解3072位RSA约需1900个逻辑量子比特。椭圆曲线需要更多量子比特，但Toffoli门数量仅为RSA的1/13。这一差异意味着，在量子计算时代，椭圆曲线密码可能比RSA更易受到攻击，尽管其经典安全性更强。这一发现为密码学选型提供了重要参考：未来高安全级别的系统可能需要结合两种密码体系的优势，或直接采用抗量子密码学方案。

05 未来展望：量子攻击与密码防御的“军备竞赛”

这项研究让我们看到了量子计算破解密码系统的清晰路径，但这并不意味着比特币等加密货币即将面临危机。从理论资源需求到实际量子计算机，仍有三大关键障碍需要跨越。

首先是量子比特的数量与质量。破解P-256曲线需要4300个逻辑量子比特，而逻辑量子比特的实现依赖量子纠错——以表面码为例，一个逻辑量子比特可能需要上千个物理量子比特，这意味着实际所需的物理量子比特数量可能达到百万级。当前最先进的量子计算机仅能提供千余个物理量子比特，且保真度远未达到要求。

其次是Toffoli门的保真度。研究表明，逻辑Toffoli门的保真度需要达到10^-9级别，而当前NISQ设备的量子门保真度多在99%左右（即10^-2级别），即便考虑量子纠错，要达到到10^-9的保真度也需要巨大的额外开销。

最后是算法的进一步优化。团队发现，模块化除法是当前算法中资源开销最大的组件，其复杂度远高于加法和乘法，未来若能在量子除法上取得突破，将大幅降低整体资源需求。此外，更灵活的量子比特拓扑结构、更高效的动态电路技术，也可能进一步压缩资源开销。

对于密码学领域而言，这项研究是一个明确的“预警信号”。尽管量子攻击尚未到来，但历史遗留的加密资产已面临长期威胁。未来，抗量子密码学的研发与部署将成为关键，而比特币等区块链系统也需要逐步升级加密协议，为量子时代的安全做好准备。

从更宏观的视角看，这项研究是量子计算从理论走向应用的重要一步。它不仅量化了量子计算破解密码的能力边界，也为量子硬件的研发提供了明确目标。随着量子技术的持续进步，密码学与量子计算的“军备竞赛”将进入新阶段，而这场竞赛的结果，将深刻影响未来数字社会的安全基石。

信息来源：“光子盒”微信公众号